"이것이 취업을 위한 컴퓨터 과학이다 with CS 기술면접" 책을 참고했습니다.
그래프는 연결 관계를 표현하는 자료구조이다. 네트워크, 운영체제 등 다양한 분야에서 범용적으로 사용하며, 알고리즘 분야에서도 자주 나오는 굉장히 중요한 자료구조라고 할 수 있다. 한 번 알아보자.
1. 그래프의 종류와 구현
그래프란 정점(vertex)이라 불리는 데이터를 간선(edge) 혹은 링크(link)로 연결한 형태의 자료구조를 의미한다. 이전 시간에 학습했던 트리구조 역시 노드와 노드를 간선으로 연결했었던 그래프의 일종으로, 노드 간의 상하 관계를 고려한 그래프라고 할 수 있다. 일반적인 그래프는 사이클(어떤 정점에서 다시 돌아올 경로가 있는 경우)을 형성하거나, 이웃한 정점끼리 별도의 상하 관계를 가지지 않는다.
그래프는 기본적으로 데이터 간의 연결 관계를 표현하는 자료구조로, 우리 일상에서 다양한 분야에 이미 활용되고 있다. 지하철 노선도나 통신 기기간의 연결 네트워크 등 꽤나 익숙한 형태로 우리에게 가까이 있다.
그래프는 앞에서 말했듯 연결 관계를 표현하기 때문에 간선이 중요한 역할을 맡으며 간선의 형태에 따라 그래프의 종류가 달라질 수 있다. 대표적인 종류는 다음과 같다.
- 연결 그래프 / 비연결 그래프 : 모든 정점이 간선으로 단 하나의 간선으로라도 갈 가능성이 존재하는지 여부
- 연결 그래프 : 그래프 상에 있는 임의의 두 정점 사이의 경로가 존재하는 그래프
- 비연결 그래프 : 어떤 정점 사이에는 경로가 없는 경우가 존재하는 그래프
- 방향 / 무방향 그래프 : 방향이 있는지 없는지 여부
- 가중치 그래프 : 간선에 가중치가 있는 그래프를 의미하며, 가중치를 비용이라고도 부른다.(정점 사이의 거리라든지)
- 서브 그래프 : 부분 그래프라도 불리며 트리에서의 부분 트리와 유사한 개념이다.
이런 그래프들의 표현 방식으로는 크게 2가지가 있다. 하나는 인접 행렬 기반으로 표현하는 것이 있고, 다른 하나는 인접 리스트로 표현하는 방식이 있다. 하나씩 알아보자.
1-2 인접 행렬 기반 그래프 표현
인접행렬 기반 그래프 표현은 N * N 크기의 단위행렬로 그래프를 표현하는 방식이다. N은 정점의 개수를 말하며, N * N 행렬의 <행, 열> 값은 <출발 정점, 도착 정점>을 의미한다. 두 정점이 연결되어 있다면 1, 그렇지 않다면 0으로 표기한다. 예를 들어 아래와 같은 그래프에 대해서 인접 행렬로 표현하면 다음과 같다.
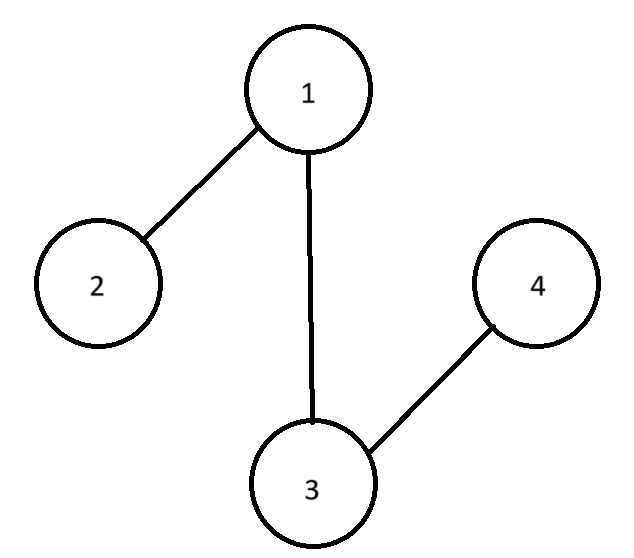
| From \ To | 1번 | 2번 | 3번 | 4번 |
| 1번 | 0 | 1 | 1 | 0 |
| 2번 | 1 | 0 | 0 | 0 |
| 3번 | 1 | 0 | 0 | 1 |
| 4번 | 0 | 0 | 1 | 0 |
방향 그래프라면 이야기가 다르겠지만, 무방향 그래프의 경우 위와 같은 특징이 존재한다. 바로 대각선 요소를 기준으로 연결 관계가 대칭을 이룬다는 점이다.(한쪽이 연결되면 From To를 뒤집어도 성립하기 때문)
만약 그래프가 가중치 그래프라면 1과 0이 아니라 1 대신 가중치를 기반으로 작성하면 된다.
1-3 인접 리스트 기반 그래프 표현
인접 리스트 기반 표현 방식은 말처럼 특정 정점과 연결된 정점들을 연결 리스트의 형태로 표현하는 방법이다. 각각의 정점마다 연결 리스트를 가질 텐데 특정 정점에서 나가는 간선에 연결된 정점들을 연결 리스트의 노드로 표현한다. 위의 예시를 인접 리스트로 표현하면 다음과 같다.
| 시작 정점 | ||
| 1 | 2 , N(가중치가 있다면) | 3 |
| 2 | 1 | |
| 3 | 1 | 4 |
| 4 | 3 |
만약 가중치 그래프라면 노드의 번호와 가중치를 묶어서 연결 리스트에 추가하면 된다.
1-4 장단점과 실제 구현
두 가지 표현 방법 모두 좋지만, 장단점을 고려해 코드를 작성하면 좋다.
| 인접 행렬 | 연결 리스트 | |
| 장점 | 간선의 존재 여부를 O(1)로 확인 가능하다. | 메모리 사용량이 O(V + E)로 희소 그래프의 경우 더 메모리를 효율적으로 사용할 수 있다. |
| 구현이 쉽다. | 간선의 순회가 더 쉽다. | |
| 단점 | 메모리 사용량이 O(V^2)로 정점 수가 많을 경우 굉장히 비효율적이다. | 간선의 존재 여부를 확인하려면 O(V) 시간 복잡도가 필요하다. |
| 희소 그래프(노드보다 간선 수가 적은 경우)의 경우 공간 낭비가 있다. | ||
| 효율성 | 밀집 그래프의 경우 용이 | 희소 그래프의 경우 용이 |
실제 코드 구현
인접 행렬
public class AdjacencyMatrixGraph {
private int[][] matrix; // 인접 행렬
private int vertices; // 정점 수
// 생성자
public AdjacencyMatrixGraph(int vertices) {
this.vertices = vertices;
matrix = new int[vertices][vertices]; // 정점 수에 맞는 2차원 배열 생성
}
// 간선 추가
public void addEdge(int source, int destination) {
matrix[source][destination] = 1; // 간선 존재
matrix[destination][source] = 1; // 무방향 그래프인 경우
}
// 그래프 출력
public void printGraph() {
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
AdjacencyMatrixGraph graph = new AdjacencyMatrixGraph(4);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.addEdge(2, 3);
System.out.println("인접 행렬:");
graph.printGraph();
}
}결과
인접 행렬:
0 1 1 0
1 0 1 0
1 1 0 1
0 0 1 0
인접 리스트
import java.util.ArrayList;
import java.util.List;
public class AdjacencyListGraph {
private List<List<Integer>> adjList; // 인접 리스트
// 생성자
public AdjacencyListGraph(int vertices) {
adjList = new ArrayList<>();
for (int i = 0; i < vertices; i++) {
adjList.add(new ArrayList<>()); // 각 정점에 대한 리스트 생성
}
}
// 간선 추가
public void addEdge(int source, int destination) {
adjList.get(source).add(destination); // 정점에 간선 추가
adjList.get(destination).add(source); // 무방향 그래프인 경우
}
// 그래프 출력
public void printGraph() {
for (int i = 0; i < adjList.size(); i++) {
System.out.print(i + ": ");
for (Integer vertex : adjList.get(i)) {
System.out.print(vertex + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
AdjacencyListGraph graph = new AdjacencyListGraph(4);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.addEdge(2, 3);
System.out.println("인접 리스트:");
graph.printGraph();
}
}결과
인접 리스트:
0: 1 2
1: 0 2
2: 0 1 3
3: 2
오늘은 그래프의 정의와 그래프를 구현하는 방법에 대해서 알아보았다. 다음 시간에는 그래프의 탐색 방법인 DFS, BFS, 그리고 다익스트라 알고리즘에 대해 차근차근 알아보자.
'Computer Science' 카테고리의 다른 글
| [CS] 4-3 자료구조. - 트리 (0) | 2024.10.23 |
|---|---|
| [CS] 4-2 자료구조. - 배열, 연결리스트, 스택 & 큐, 해시 테이블 (2) | 2024.10.17 |
| [CS] 4-1. 자료구조 - 개요 (0) | 2024.10.11 |
| [CS] 3-3. 운영체제 - 가상 메모리, 파일 시스템 (0) | 2024.10.09 |
| [CS] 3-2. 운영체제 - 동기화와 교착 상태, CPU 스케줄링 (4) | 2024.10.05 |
